Le sujet de cet article est le calcul d'un auvent en polycarbonate de vos propres mains. Il faut apprendre à calculer les principaux paramètres de la structure liés à sa résistance et ses dimensions. Alors allons-y.

Que calcule-t-on
Il faut apprendre à calculer :
- L'épaisseur du polycarbonate et le pas de la caisse en fonction de la charge de neige prévue par mètre carré.
- Dimensions du couvercle de l'arche (ce qui en termes de géométrie revient à calculer la longueur de l'arc).
Pour clarifier: nous explorons des moyens de calculer l'arc pour un rayon et un angle connus du secteur, ainsi que pour le cas où nous ne connaissons que les distances entre les points extrêmes de la surface de l'arc.
- Section de tuyau minimale avec une charge de flexion connue.
Dans cet ordre, nous allons continuer.
Lattage et épaisseur de revêtement
Commençons par le calcul de la charge de neige.
Avant de comprendre comment calculer un auvent en polycarbonate, nous formulerons quelques hypothèses sur lesquelles le calcul est basé.
- Les données fournies sont pertinentes pour un matériau de haute qualité sans signes de destruction par le rayonnement ultraviolet. Le polycarbonate sans filtre UV devient cassant après 2-3 ans de fonctionnement à la lumière.

- Nous négligeons délibérément la stabilité à la déformation limitée de la caisse, la considérant comme absolument solide.
Et maintenant - un tableau qui vous aidera à choisir l'épaisseur optimale de polycarbonate et le pas de la caisse.
| Charge, kg/m2 | Dimensions des cellules de la caisse avec épaisseur de polycarbonate, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050x750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Cambre
Calcul par rayon et secteur
Comment calculer l'arc d'un auvent si l'on connaît le rayon de courbure et le secteur d'arc ?

La formule ressemblera à P=pi*r*n/180, où :
- P est la longueur de l'arc (dans notre cas, la longueur d'une feuille de polycarbonate ou d'un tuyau profilé, qui deviendra un élément du cadre).
- pi est le nombre "pi" (dans les calculs qui ne nécessitent pas une précision extrêmement élevée, généralement pris égal à 3,14).
- r est le rayon de l'arc.
- n est l'angle de l'arc en degrés.
Par exemple, calculons de nos propres mains la longueur de l'arc de la canopée avec un rayon de 2 mètres et un secteur de 35 degrés.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 mètre.
Au cours du travail, la situation inverse se produit souvent: il est nécessaire d'ajuster le rayon et le secteur de l'arc à une longueur fixe de l'arc. Les raisons sont claires : le prix du polycarbonate est suffisamment élevé pour minimiser la quantité de déchets.
Évidemment, dans ce cas, le produit du secteur et du rayon sera égal à P/pi*180.
Essayons de placer l'arche sous une tôle standard de 6 mètres de long. 6/3.14*180=343.9 (avec arrondi). De plus - une simple sélection de valeurs avec une calculatrice en main: par exemple, pour un secteur d'arc de 180 degrés, vous pouvez prendre le rayon égal à 343,9 / 180 \u003d 1,91 mètres; avec un rayon de 2 mètres, le secteur sera égal à 343,9 / 2 \u003d 171,95 degrés.
Calcul par accords
À quoi ressemble le calcul de la conception d'un auvent en polycarbonate avec une arche si nous ne disposons que d'informations sur la distance entre les bords de l'arche et sa hauteur?
Dans ce cas, la formule dite de Huygens est appliquée. Pour l'utiliser, divisons mentalement la corde reliant les extrémités de l'arc en deux, après quoi nous dessinons une perpendiculaire à la corde au milieu.
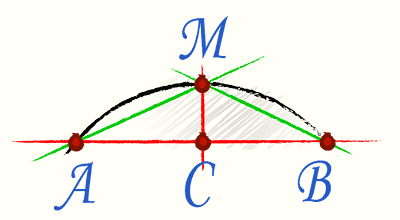
La formule elle-même a la forme Р=2l+1/3*(2l-L), où l est l'accord AM et L est l'accord AB.
Important : le calcul donne un résultat approximatif. L'erreur maximale est de 0,5 % ; plus le secteur angulaire de l'arc est petit, plus l'erreur est petite.
Calculons la longueur de l'arc pour le cas où AB \u003d 2 m et AM - 1,2 m.
P=2*1.2+1/3*(2*1.2-2)=2.4+1/3*0.4=2.533 mètres.
Calcul de la section avec une charge de flexion connue
Tout à fait une situation de vie : une partie de la voilure est une visière de longueur connue. Nous pouvons estimer grossièrement la charge maximale de neige sur celle-ci. Comment choisir un tube profilé d'une telle section pour les poutres afin qu'il ne se plie pas sous la charge?

Note! Nous n'abordons délibérément pas la façon de calculer la charge sur la voilure. L'évaluation de la charge de neige et de vent est un sujet complètement autonome pour un article séparé.
Pour calculer, nous avons besoin de deux formules :
- M = FL, où M est le moment de flexion, F est la force appliquée à l'extrémité du levier en kilogrammes (dans notre cas, le poids de la neige sur la visière), et L est la longueur du levier (la longueur de la poutre qui supporte la charge de la neige, d'un bord à l'autre des attaches) en centimètres.
- M/W=R, où W est le moment de résistance et R est la résistance du matériau.
Et comment ce tas de valeurs inconnues va-t-il nous aider ?
En soi, rien. Certaines données de référence manquent pour le calcul.
| nuance d'acier | Force (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Référence : Les aciers St3, St4 et St5 sont généralement utilisés pour les canalisations professionnelles.
Maintenant, sur la base des données dont nous disposons, nous pouvons calculer le moment de résistance à la flexion du tube profilé. Faisons cela.
Supposons que 400 kilogrammes de neige s'accumulent sur un auvent de deux mètres avec trois poutres porteuses en acier St3.Pour simplifier les calculs, nous conviendrons que toute la charge tombe sur le bord de la visière. Évidemment, la charge sur chaque poutre sera de 400/3 = 133,3 kg ; avec un levier de deux mètres, le moment de flexion sera égal à 133,3 * 200 \u003d 26660 kgf * cm.
Nous calculons maintenant le moment de résistance W. De l'équation 26660 kgf * cm / W = 2100 kgf / cm2 (résistance de l'acier), il s'ensuit que le moment de résistance doit être d'au moins 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Comment la valeur du moment de résistance nous conduira-t-elle aux dimensions du tuyau ? À travers les tableaux d'assortiment contenus dans GOST 8639-82 et GOST 8645-68 réglementant les dimensions des tuyaux carrés et en forme. Pour chaque taille, ils indiquent le moment de résistance correspondant, et pour une section rectangulaire - le long de chacun des axes.
Après avoir vérifié les tableaux, nous constatons que la taille minimale d'un tuyau carré avec les caractéristiques requises est de 50x50x7,0 mm; rectangulaire (avec orientation verticale du plus grand côté) - 70x30x5,0 mm.

Conclusion
Nous espérons que nous n'avons pas surmené le lecteur avec une abondance de chiffres secs et de formules. Comme toujours, des informations supplémentaires sur les méthodes de calcul et de conception des auvents en polycarbonate sont disponibles dans la vidéo de cet article. Bonne chance!
L'article vous a-t-il aidé ?